「ガウスの消去法」は一次連立方程式を解くための1つの方法ではあるが、 これは必ずしも「計算を楽にするため」に勉強しているのではなく、 「後の話を理解するために必要だから」勉強しているものなので、 「別に他のやり方でも解けるし」などと考えることなく、 この解法をしっかりマスターして欲しい。中学生の諸君。「中2数学」で差がつくポイント、「連立方程式」にはコツがあるぞ。(ビシッ)差がつくのはココだ!(ビシッ)トォォォ~ッ! オール5家庭教師、見参ッ! 加減法、代入法どっちも来い! 文章題も! 勝負の無料サイトだ。 連立方程式は、未知数が2つというのがネックになっています。1つになれば、普通の方程式として解くことができる訳ですから、 何とかして未知数を1つにする ことが、連立方程式の解き方の基本となります。 それぞれ見ていくことにしましょう。 代入法

いろいろな連立方程式 中学生 数学のノート Clear
連立方程式 やり方
連立方程式 やり方-連立方程式の解き方 2つの式から x や y の値を求めることを 連立方程式 (れんりつほうていしき)と言います。例えば、連立方程式を文章問題にすると以下連立方程式の解き方(加減法 (1)) 大きな区分 中学数学 (←Top) >> 中学2年 >>連立方程式 現在地 と前後の項目 は最小限のセット **代入法による解き方** 連立方程式の代入法1



Studydoctor連立方程式の解き方 加減法 中2数学 Studydoctor
連立方程式を解く 連立方程式を解くには,xかyのどちらかの文字を1つ消去して,文字が1つだけの方程式にして解く。 この解き方に加減法と代入法がある。 加減法 x,またはyの係数をそろえて2つの式を 「たす」または「ひく」して文字を一つ消す。連立方程式の解き方 連立方程式の解き方は、下記の2つがあります。 加減法 ⇒ 1つの未知数が消えるように2つの方程式を加減し、もう一方の未知数の解を求める方法 代入法 ⇒ 1つの式を「x=」の形にして、もう一方の式に代入し解を求める方法(1)鶴亀算を問題に出し、連立方程式で解く。 (2)銀林ダイアグラムを示し、連立方程式で解く意味を説明する。 (3)解と答えの違いを説明する。 (4)計算の意味は「全てを鶴とする」ことと対応する事を説明する。 (5)だから、計算すれば必ず答えが出ることを示す。
復習連立方程式の解き方 連立方程式とは、一般的に \begin{eqnarray}\left\{\begin{array}{l}axby=c\\dxey=f\end{array}\right\end{eqnarray} といった形で表すことが多い式です。 2元1次方程式と呼ばれる「2つの変数(文字)」と「最大次数が1」の式で表されます。 連立方程式の解き方は大きく2つあります。それは、先日連立方程式の解き方のコツ で、連立方程式は加減法、代入法があり、どちらのやり方でも解ける。 学校でもこの2つのやり方を勉強します。 そして、まずは加減法をしっかり学習しましょうとお話の2つだったよね。 どっちを使うかわからないときは、 連立方程式の解き方のコツをみてみてね^^ 分母をはらったあとの連立方程式、 $$2x y = 4$$ $$3x 2y = 5$$ は「加減法」を使って解いてくよ!
小数点の連立方程式解き方をイチから解説してくぞ! kaztaro ゆい 小数があるときってどうすればいいんだっけ? かず先生 10倍、100倍して小数を消せばいいよ! というわけで、今回の記事では「小数を含む連立方程式の解き方」についてイチから解説していきます。 今回の記事で これは普通の連立方程式で、何も難しくはありませんね。例えば、次のような連立方程式を考えてみましょう。 $$\begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 1 \\ 3 \end{bmatrix}$$この問題では(1)を4倍すると −12y ができ、(2)を3倍すると 12y ができるので、足し算により y が消去できて x だけの方程式になります。→(3) →(3) (3)の結果を(1)か(2)のどちらかに代入すると、もう一つの未知数も求まります。



この問題の連立方程式の解き方を教えて欲しいです これを授業 Yahoo 知恵袋




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット
LU分解と連立方程式 LU分解を使って $A\overrightarrow{x}=\overrightarrow{b}$ という連立方程式を解くことができます。 手順1.$A$ のLU分解を求める。 $A=LU$ なる $L$ と $U$ を求めます。求め方は後述します。 手順2.$LU\overrightarrow{x}=\overrightarrow{b}$ を解く。 単元 連立方程式とその解き方, 「めっちゃ字汚いし、見づらいです! あとりんごとみかんの絵きもいけど許してください! すみませんm(__)m」, 学年 中学2年生, キーワード 連立方程式二元連立方程式 関数電卓が手元にないとき、面倒事を押し付けれて非常に助かります。 sqrt (値)のように使用します。 連立方程式の問題の答え合わせ。 とても便利でしたが途中の式や、分数表示ができない点が残念でした。 宿題の答え合わせに使い




分数をふくむ連立方程式 Youtube




連立方程式の2つの解き方 代入法 加減法 数学fun
連立方程式とは2つの文字(xとy)を含み、2つの式からなる方程式のこと。 連立方程式の解き方には 代入法 と 加減法 がある。 どちらの場合もxかyのどちらか 1つの文字を消去して解く 。 代入法 ≫ 加減法 片方の式が x = の形になっていれば、それを他方のxに代入することでxが消えてyだけの方程式ができる。 (y= の形ならyに代入する。 連立方程式の解き方の鉄板である「消去法」をおさらいした上で、それを行列で考えます。 サイト内検索 あらゆるワードの関連記事を検索できます! おぐえもん 情報系大学院の出身です♪Webサイトやチラシ、冊子などのデザインや、システム開発などの経験があります。音楽が好きで \(a,b\) を含まない方程式を取り出し、新たに連立方程式をつくる。 ①の連立方程式を解き、共通する解を求める ②で求めた解を、\(a,b\) を含む方程式に代入し連立方程式を作る
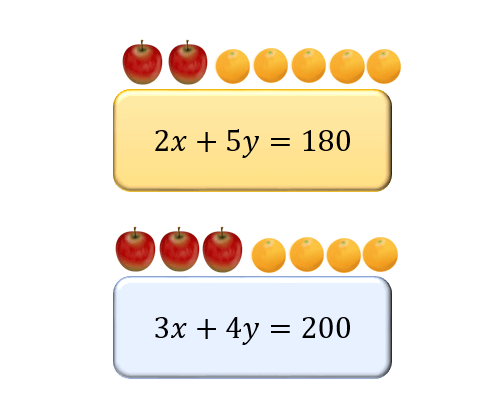



連立方程式 加減法 の解き方 なぜ加減法が成り立つか アタリマエ



1
連立方程式の文章題は「最後の一文」から読んでみてね^_^ Step2 等式を2つ作る! 文字2つで連立方程式をつくっちゃおう。 あとは連立方程式の解き方さえわかれば大丈夫。 2つの等しい関係をみつけられるかが勝負だ。 例題をみてみよう。通常の方法では、この連立方程式を解くには、まず以下のように「 (2)− 2× (1) ( 2) − 2 × ( 1) 」 を行うことで y y の値を得ます。 2x 4y = 22 −) (2x 2y = 18) =) 2y = 4 =) y = 2 2 x 4 y = 22 −) ( 2 x 2 y = 18) =) 2 y = 4 =) y = 2 これで y = 2 y = 2 であることがわかりました。 後は、この y y の値を x = 9 −y x = 9 − y にあてはめると x = 9− 2 = 7 x = 9 − 2 = 7 であることがわかります。 解き方 numpylinalgsolve を使って次のように計算できる。 結果は次のとおりとなる。 array ( 1, 2, 3 ) 1組の 連立方程式 を単発で解く場合は上の方法で問題ないが、 A の部分は変わらずに b が変わる場合を数多く解く場合には次のLU分解を使うやり方のほう




中学数学 連立方程式 加減法 中学数学の無料オンライン学習サイトchu Su




連立方程式の解き方 移項と展開 Youtube
連立方程式には「 加減法 」「代入法」と2つの解き方があります。 この2つのうち、苦手としている人が多いのが今回取り上げる代入法を使った解き方です。 実際には、加減法だけを使えれば何とか乗り切ることはできます。 だけど、代入法を知っておいた方が圧倒的に便利です。 今後学習していくであろう関数の分野で、代入法は大活躍するということ 連立方程式は掃出法と言われるやり方で機械的に解くことができます。 まず、4つの式のうちaの係数の絶対値がが最も小さいものを選びます。複数ある場合はどれでもいいです 今回ならば①式です 次に、その①式を何倍かして残りの3つの式のaを消去します 次に、いまaを消した式に対し 連立方程式の問題は、答えがあっているかどうかを簡単に確かめることができます。yを求めるためにx=3を代入した式と違う式(今回は3x2y=3)に、x=3とy=3を代入してみましょう。 $$3 \times 3 2 \times 3 = 3\\9 6 = 3\\3 = 3$$
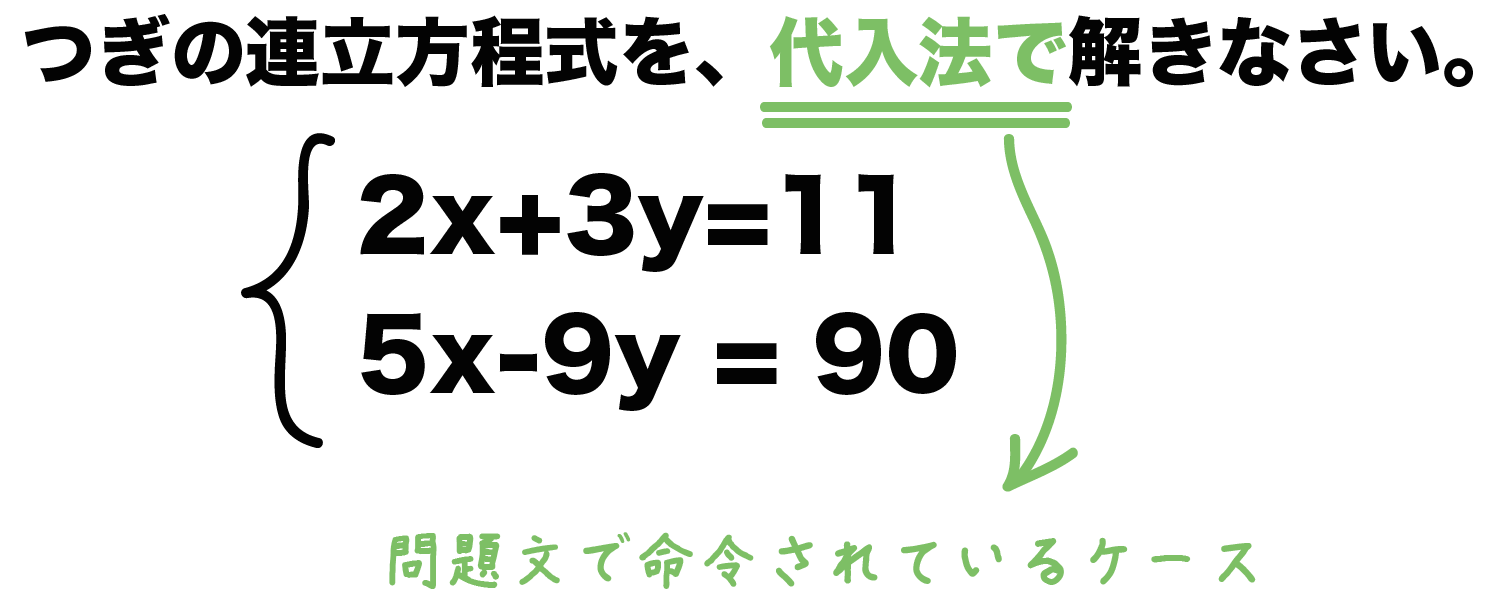



超簡単 連立方程式の解き方を見分ける2つのコツ Qikeru 学びを楽しくわかりやすく




中学数学の解説21ページ目 三重の個人契約家庭教師
二つのやり方で,同じ解になることを確認しなさい。 両方を何倍かして加減する (5) − =− − = 4 3 3 23 x y x y (6) = − = 3 2 4 4 5 13 x y x y 同じ答えが出ることを確認し,解法の比較をしましょう。 連立方程式③ 連立方程式の解き方(1)C 学 年 年 年 組 氏名 学習日: 月 日( ) 中学校 ちょっと弟が連立方程式のやり方が分からないというので問題を見てたんですが、私も忘れてます、、、。で、問題なのですが、{ 3x 2y = 8 5x 3y =7という問題なのですが、すみませんがやり方を教えてくれるとありがた連立方程式を 代入法で解く方法 について解説していくよ! 連立方程式を解くためには 『加減法』と『代入法』という2つの解き方があったよね。




連立方程式の解き方 加減法 代入法と文章題の計算方法 リョースケ大学




中2数学 カッコ 分数を含む連立方程式 例題編 映像授業のtry It トライイット




連立方程式の解き方 加減法 Youtube




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者




連立二元一次方程式をいろいろな方法で解いてみよう 身勝手な主張
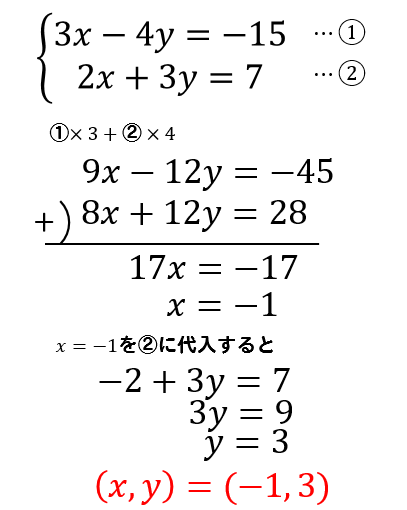



連立方程式 加減法の解き方をわかりやすく問題を使って徹底解説 数スタ



第1章 連立方程式




分数の連立方程式 解き方は両辺に数をかけて分母を消すんだ 中学や高校の数学の計算問題




徹底解説 連立方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ



U9j580gf8iba369ji2w Xyz P 703




中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu
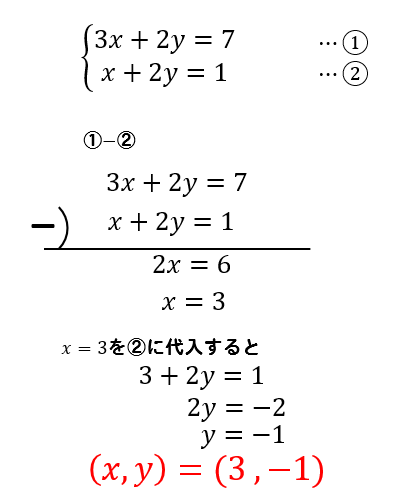



方程式の高校入試問題 連立方程式 方程式の解き方まとめサイト
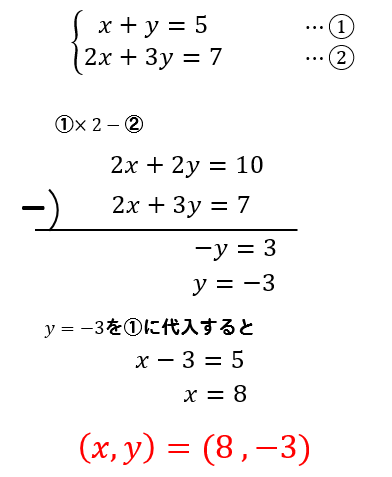



方程式練習問題 連立方程式 A B C 方程式の解き方まとめサイト



連立方程式の解き方 Gains ゲインズ ネットスクールの資格取得応援情報サイト




連立方程式の解き方 Youtube




方程式の種類と解き方 中学で学習する方程式ってどんなのがある 中学数学 理科の学習まとめサイト




連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト



Studydoctorかっこのついた連立方程式 中2数学 Studydoctor
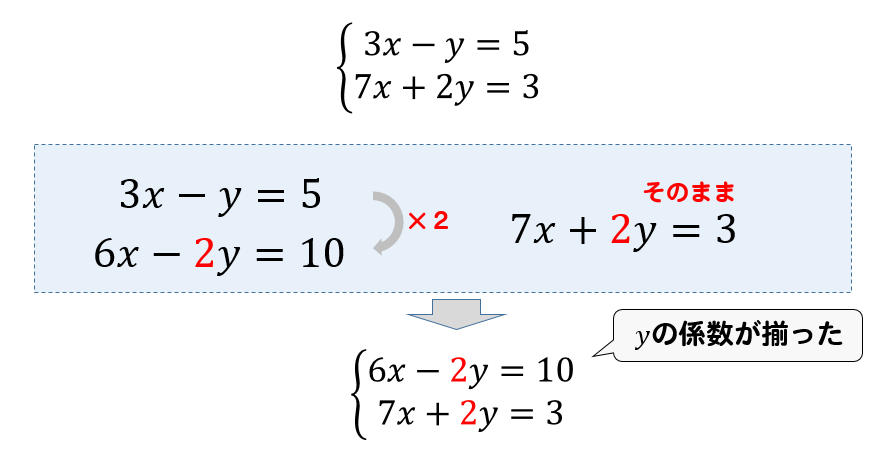



連立方程式 加減法を使った問題の解き方は やり方をイチから解説 方程式の解き方まとめサイト




連立方程式 連立方程式の加減法と代入法 中学数学 定期テスト対策サイト




加減法 連立方程式の解き方 中学数学 By じょばんに マナペディア




数学の連立方程式のやり方が分かりません 教えてくれると有難いです Clear




解き方 連立方程式の加減法がわかる4つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 連立方程式 の効果的な教え方 導入と指導上の注意点



連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典




中2数学 a b cの連立方程式 練習編 映像授業のtry It トライイット




3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ




中学2年数学 連立方程式 加減法を使った連立方程式の解き方 実際に問題を解きながら解説 数学の面白いこと 役に立つことをまとめたサイト
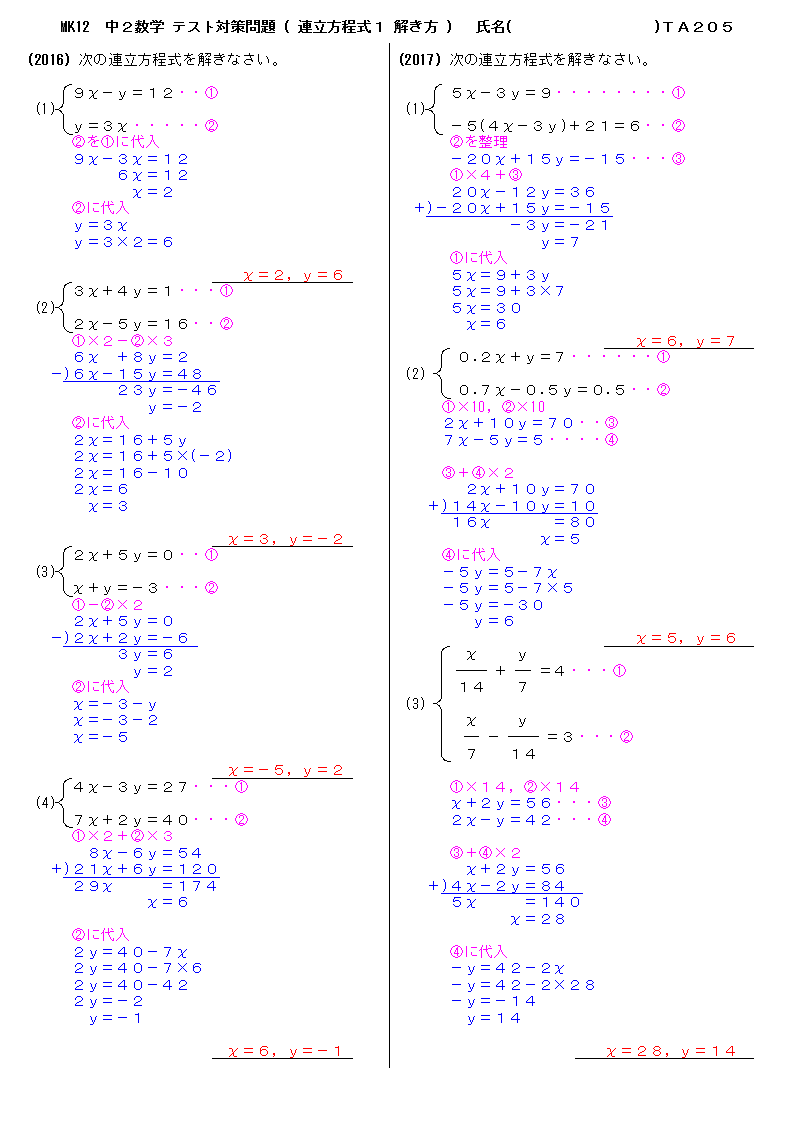



無料 中2数学 テスト対策 解答プリント 5 連立方程式1 解き方
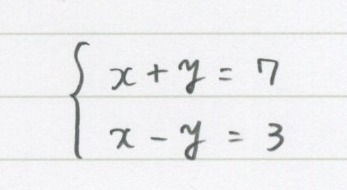



5 1 連立方程式 基本 勉強できようサイト




高校数学で学習する連立方程式の解き方まとめ 数スタ



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料



連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス
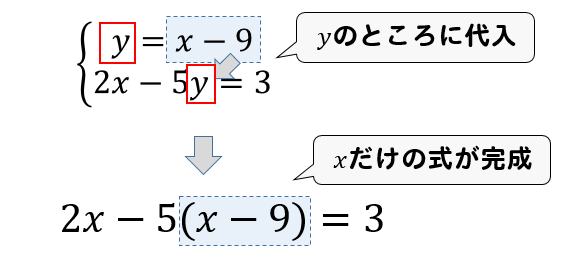



連立方程式 代入法を使った問題の解き方は やり方をイチから解説 方程式の解き方まとめサイト
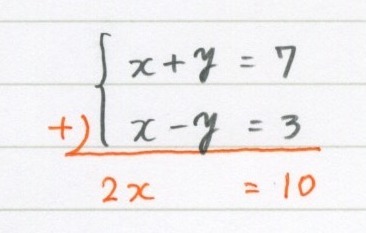



5 1 連立方程式 基本 勉強できようサイト




連立方程式の利用の問題の解き方 代金の問題 1 現役塾講師のわかりやすい中学数学の解き方




連立方程式 加減法の問題です 問題集の答えです 波線までは分かる 数学 教えて Goo




都立入試コラム第1弾 連立方程式の解き方 タダゼミ 杉並 大学生による無料の都立高校合格講座




連立方程式を小学生に教える




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット
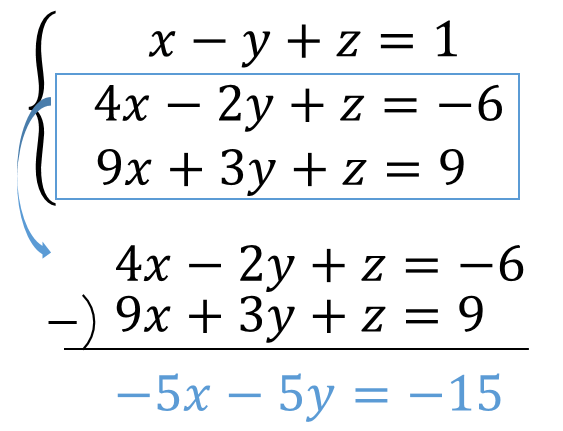



連立方程式 3つの文字 式の問題を計算する方法は 数スタ




連立方程式 1 代入法と加減法 バカでもわかる 中学数学




お勉強 連立方程式の解き方のご提案 去年の男子女子x y人の問題 そらの暇つぶしch
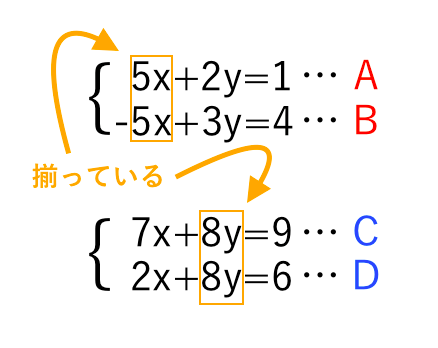



連立方程式の解き方 加減法 苦手な数学を簡単に



1




連立方程式の解き方 代入法 Youtube




数学 中2 15 連立方程式 加減法の基本編 Youtube




連立方程式の解き方と交点の座標の求め方 数学の偏差値を上げて合格を目指す




例題付き 連立方程式の解き方と失敗しないコツ




3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




小数の連立方程式 Youtube




連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト



連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料



1




中2 数学 連立方程式の解き方二通りを解説 授業動画あり アオイのホームルーム




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者




いろいろな連立方程式 中学生 数学のノート Clear




小数の連立方程式の解き方 両辺を10倍や100倍しよう 中学や高校の数学の計算問題




連立方程式の問題 高校の範囲でも登場する大切な分野だ 中学や高校の数学の計算問題




お勉強 連立方程式を楽に解く 数学は楽してなんぼ そらの暇つぶしch




連立方程式を解く時の流れを行列に当てはめてみよう 線形代数を宇宙一わかりやすく解説してみるサイト




高校数学 2式が互いに対称な連立方程式 和と差で組み直せ 受験の月



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料



たかが連立方程式ではあるけれど 大験セミナー わくわく日記
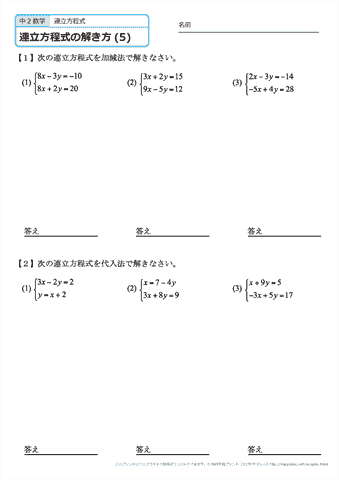



中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



連立方程式です やり方を教えて頂けませんか Yahoo 知恵袋




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




3分でわかる 小数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく



第1章 連立方程式
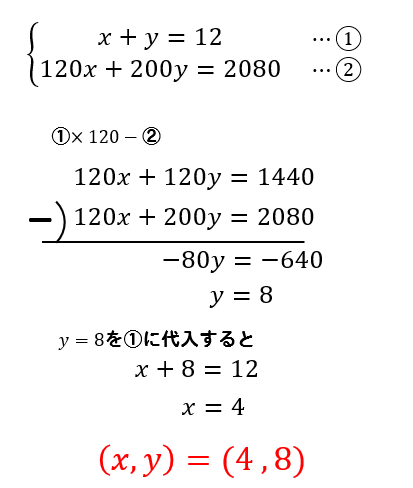



連立方程式の利用 文章問題 解き方まとめ 方程式の解き方まとめサイト



Studydoctor連立方程式の解き方 加減法 中2数学 Studydoctor
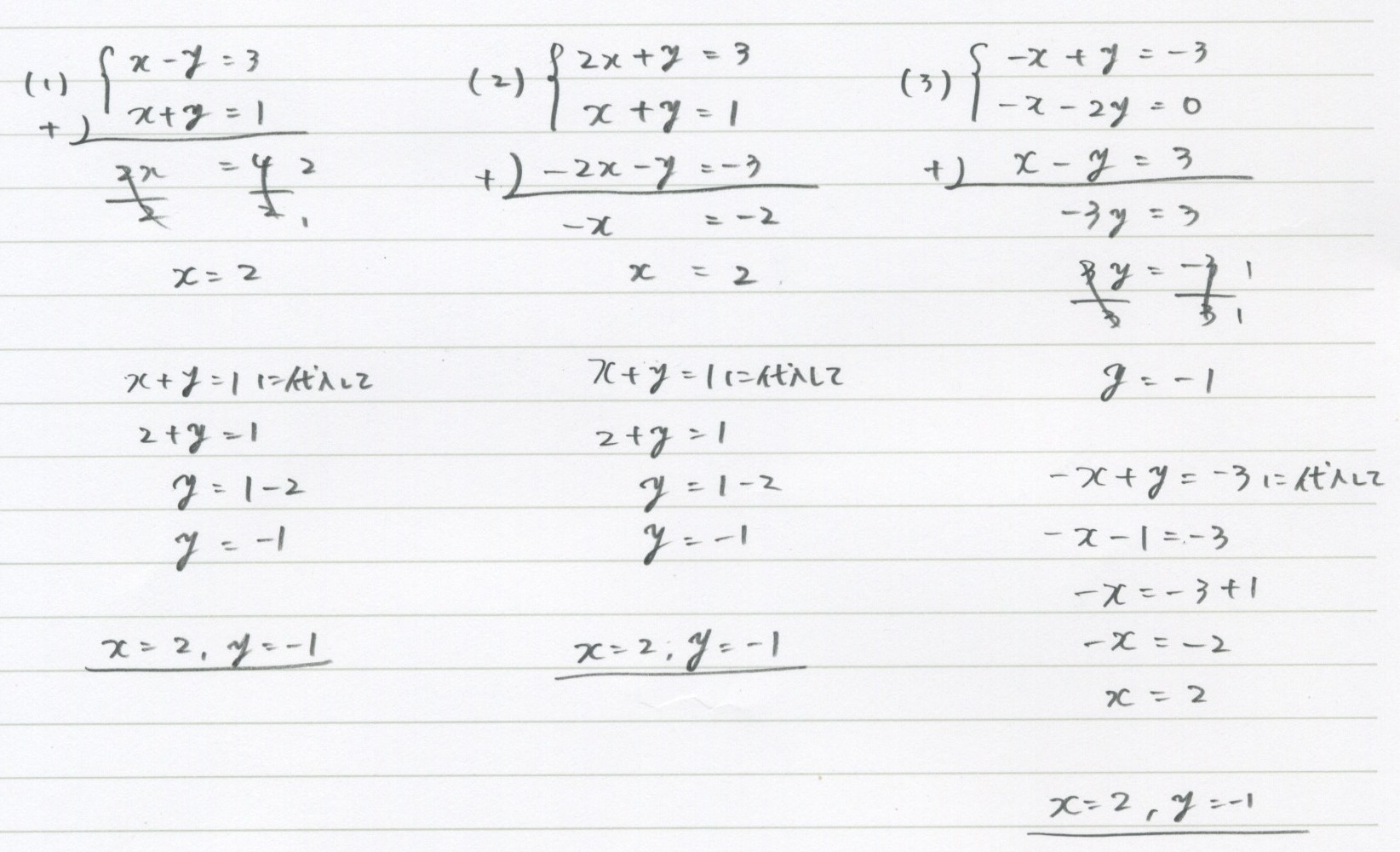



5 1 連立方程式 基本 勉強できようサイト
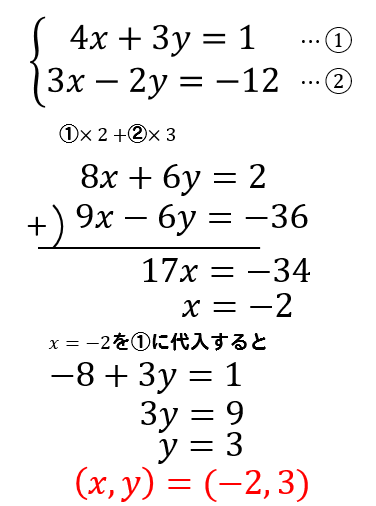



連立方程式 加減法 代入法の簡単な練習問題 これでテストはバッチリ 数スタ
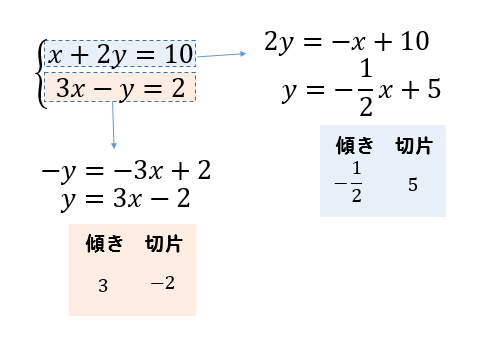



連立方程式 グラフの交点を使って解を求める問題は 書き方をイチから解説 方程式の解き方まとめサイト




連立方程式の解き方 問題の文字を消すことが解き方のコツだ 三重の個人契約家庭教師



連立方程式の解き方



連立方程式 その1 名古屋市北区の学習塾は思考力を育む 泰成スクール




連立方程式の利用の問題の解き方 割合の問題 5 現役塾講師のわかりやすい中学数学の解き方
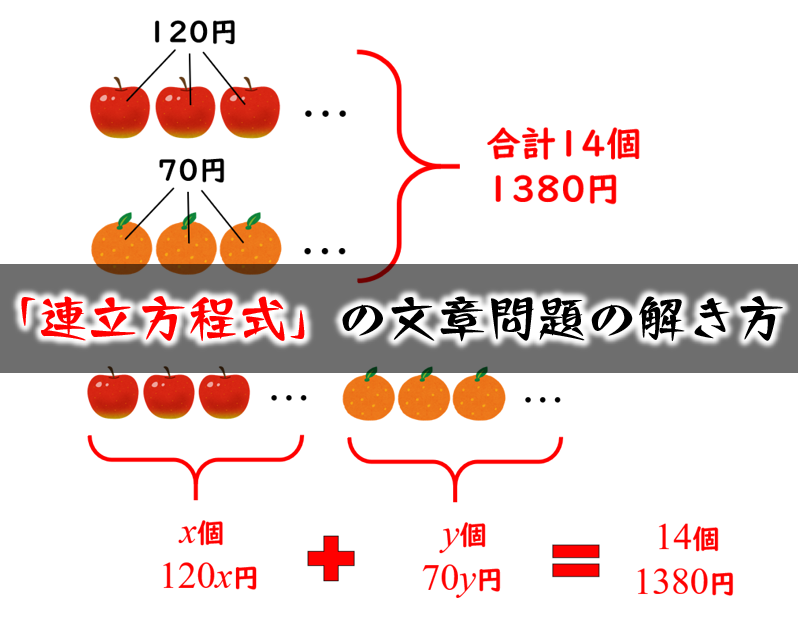



連立方程式の文章問題の解き方 数学fun



連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点
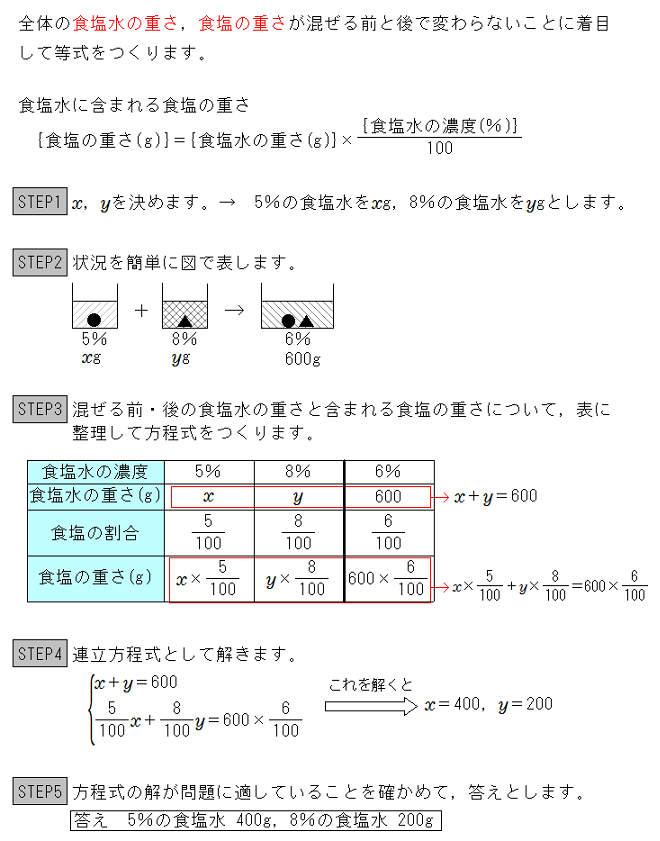



連立方程式 食塩水の問題で連立方程式をつくるコツ 中学数学 定期テスト対策サイト




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学




3つの連立方程式の問題 解き方はこのようにすればバッチリだ 中学や高校の数学の計算問題



連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料



連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料




連立方程式の加減法の解き方をマスターしたい方は見てください 中学や高校の数学の計算問題




連立方程式 問題 Youtube




中学数学 連立方程式 の効果的な教え方 小数 分数問題




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook




中学数学2年 連立方程式の解と係数 受験の月



1




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




こんな風に なぜ連立方程式で交点がわかるんですか Clear


